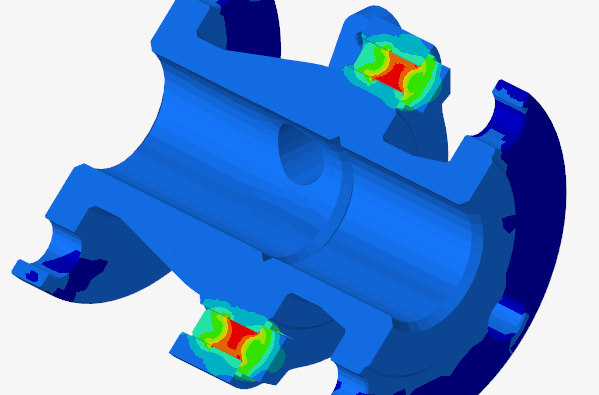
A Short Review of Simulative Connection Assessment
Connections and joints are often the weakest links in mechanical assemblies, making their validation a critical part of structural simulation. Finite element models can evaluate bolts, welds, rivets, snap-fits, and adhesive bonds under realistic loads. By simulating how joints carry forces, engineers ensure reliability, safety, and performance before manufacturing.
Typical Goals and Targets in Joint and Connection Analysis
The primary goal of connection analysis is to confirm that fasteners and joints can safely transmit loads without loosening, yielding, or failing over time. Engineers use simulation to study stress concentrations, preload effects, fatigue life, and failure modes in bolted or welded connections. For bonded joints, the focus is on shear and peel stresses, while for snap-fits it’s on deformation and retention forces. Proper validation ensures that the integrity of the entire structure is not compromised by its connections.
Core Modeling Dimensions in Joint Validation Simulations
Most joint models require nonlinear approaches because of contact, friction, and material plasticity. While simple linear spring elements can approximate joint stiffness, they often underestimate localized stresses. Nonlinear joint analysis provides a more realistic picture of preload loss, slip, and stress redistribution.
Connection validation can be performed under static loads (e.g., coupled tension-torque on a bolt) or transient conditions (e.g., dynamic vibration on a fastener). Static analysis ensures joints meet design loads, while transient studies capture load cycling and preload relaxation. Time-dependent behavior is crucial for durability predictions.
Most joint validation problems are solved with implicit solvers due to their ability to handle static and quasi-static loads. However, explicit solvers may be used for crash, drop, or impact scenarios where joint performance under high strain rates is critical. The solver choice depends on whether the joint behavior is slow and quasi-static or fast and highly dynamic.
Bolted and riveted joints are often modeled with elastic-plastic material laws to capture yielding under high loads. Welds and adhesives may require cohesive zone or damage models to predict crack initiation and propagation. The correct material law ensures realistic simulation of joint failure mechanisms.
Simplified joints may be modeled as beam or spring elements for system-level stiffness evaluation. Detailed analyses use 3D solid elements with contact definitions to capture local stress distribution. The level of geometric detail chosen should balance computational cost with accuracy.
Joint performance can be influenced by multiple physical effects. Thermal expansion can alter bolt preload, while fluid pressure may act on seals or flanges. In electronics or aerospace, electromagnetic heating can also affect adhesive strength. Coupled multiphysics ensures realistic predictions under operating conditions.
Deterministic joint validation assumes fixed preload and material properties, while probabilistic methods account for variability in torque, surface friction, or material strength. Reliability studies using statistical simulations help engineers design joints that remain safe under real-world uncertainties.
Connections may be modeled in 1D using connector elements for global stiffness studies, in 2D cross-sections for weld seams, or in full 3D for bolts and adhesives. The dimensionality chosen affects computation time but also the ability to capture localized stress effects accurately.
Joints are often subject to cyclic or vibratory loads. Frequency-domain analysis (modal or harmonic) evaluates how joints influence system dynamics, while time-domain fatigue analysis predicts life under varying loads. Combining both approaches provides insight into both resonance and durability.
Parametric studies can vary bolt diameter, weld length, or adhesive thickness to optimize connection performance. Automated DOE (Design of Experiments) studies help identify the most influential design variables. This reduces overdesign while ensuring safety margins are maintained.
Nonlinear joint simulations can be numerically challenging due to contact convergence issues. Iterative solvers with load incrementation and contact stabilization often improve stability. Choosing the right solver strategy avoids non-convergence and ensures reliable results.
Continuum models capture detailed stress states in bolts, welds, or adhesive layers. Discrete connector elements, by contrast, are efficient for system-level analysis where local detail is less important. Hybrid approaches often combine discrete models for global stiffness with continuum submodels for local stress validation.
Typical Mistakes in Joint Validation and How to Avoid Them
Common mistakes include applying unrealistic bolt preload, neglecting friction effects, or simplifying welds and adhesives too aggressively. Overly rigid connection models can give misleading stress predictions, while insufficient mesh refinement fails to capture local stress peaks. To avoid errors, engineers should calibrate models with test data, perform mesh convergence studies, and carefully define contact conditions.
Your Joint Analysis and Simulation Project with FiniteNow
Use Cases for Joint and Connection Simulation
Bolted Flange Analysis in Pressure Vessels
FE simulation verifies that flange bolts maintain preload under internal pressure, thermal expansion, and vibration. The study identifies risk of leakage or bolt relaxation, ensuring compliance with industry codes.
Welded Joint Validation in Vehicle Frames
Weld seam simulations predict stress concentrations and potential fatigue crack initiation points in automotive body structures. This helps engineers reinforce weld paths without unnecessary material addition.
Adhesive Bonding in Lightweight Structures
In aerospace and automotive composites, adhesive joint models predict peel and shear failure under combined thermal and mechanical loads. Validation ensures long-term reliability while supporting lightweight construction.
Learn more about our portfolio of Structural Engineering Services
FAQ – Connections and Joint Validation by Finite Element Simulation
Connection validation is the process of using finite element models to analyze how joints such as bolts, welds, rivets, or adhesives behave under load. It ensures that connections safely transfer forces without loosening, slipping, or failing. Since joints often govern overall system reliability, their accurate simulation is essential for predicting product performance.
While individual components may be strong, the overall structure is only as reliable as its connections. Joints are often stress concentrators and can be subject to preload relaxation, fatigue, or failure. Validating joints ensures the entire assembly works as intended and avoids costly failures in service.
Commonly simulated joints include bolted and riveted fasteners, welded seams, bonded adhesive layers, press-fits, and snap-fits. Each requires different modeling techniques depending on load transfer mechanisms. Advanced models even combine multiple connection types, such as bolts with adhesive bonding, to replicate real-world hybrid joints.
The accuracy depends on how well contact, preload, and material properties are represented. For bolted joints, torque-preload relationships and friction coefficients must be realistic. When calibrated with experimental data, FE-based joint validation can closely match test results and significantly reduce the number of physical prototypes needed.
Linear models treat joints as simple springs or rigid connectors, which may be sufficient for early design stages. Nonlinear simulations include effects such as contact separation, frictional slip, and plastic deformation, providing far more realistic predictions. Most practical joint validation requires nonlinear approaches to capture real-world load transfer behavior.
Preload determines how much initial clamping force a bolt applies, directly affecting joint stiffness and load distribution. Friction influences whether a joint resists sliding or begins to slip under load. Incorrectly modeling preload or friction can lead to significant errors in predicted safety margins and fatigue life.
Preload determines how much initial clamping force a bolt applies, directly affecting joint stiffness and load distribution. Friction influences whether a joint resists sliding or begins to slip under load. Incorrectly modeling preload or friction can lead to significant errors in predicted safety margins and fatigue life.
A frequent mistake is to model welds or adhesives as perfectly rigid, which underestimates stress concentrations in surrounding materials. Over-simplification can hide potential crack initiation sites. The use of cohesive zone models or fracture mechanics approaches allows engineers to simulate realistic failure initiation and progression in welded and bonded joints.
Fatigue prediction combines stress or strain results from the joint simulation with S–N curves or damage models. Bolted joints are checked for preload relaxation and fretting fatigue, welds for crack initiation at the toe, and adhesives for delamination. Accurate fatigue assessment requires both high-fidelity simulation and test data for calibration.
FiniteNow.com offers instant online quoting for fast project initiation, eliminating lengthy proposal processes. Projects are executed by a scalable pool of experienced FEA specialists who have domain knowledge in fastening, welding, and bonding. By leveraging a network of pre-audited simulation providers, FiniteNow delivers cost-competitive solutions while maintaining consistent quality and reliability.
Hybrid joints are simulated using a combination of discrete fastener models and continuum adhesive layers. This approach captures the load-sharing between bolts and bonded regions under static, fatigue, and thermal cycling. Accurate hybrid modeling allows engineers to design lightweight but robust assemblies, especially in aerospace and automotive structures.
Nonlinear joint simulations often face difficulties with contact convergence. Advanced analysts mitigate this by applying step-wise loading, adjusting contact stabilization, and refining mesh in high-stress regions. Arc-length methods or augmented Lagrangian approaches may be used when solving complex preload relaxation or slip-stick transitions.
In aerospace, automotive, and energy sectors, joint simulations are validated through a combination of targeted experiments, benchmark comparisons, and sensitivity studies. Engineers correlate FE results with physical testing under controlled conditions, such as bolt torque checks or weld fatigue tests. This rigorous validation ensures compliance with certification standards and builds confidence in simulation-driven design decisions.
Start Now! It will only take 12 minutes
It has never been faster, easier and more cost effective to get a quotation for your structural simulation needs:
Looking for more details and background about Connections and Joints Modelleling?
Practical Modelling of Joints and Connections in FEA
The Textbook Section
Introduction
Most real-world structures are held together by connections. Whether it is the millions of rivets securing the skin of an aircraft, the spot welds along an automotive body-in-white, or the heavy bolts clamping together a gearbox housing, joints and connections form the backbone of structural integrity. They are everywhere, and in many cases, they are the limiting factor in both strength and fatigue performance.
For the engineer engaged in Finite Element Analysis (FEA), joints pose a persistent dilemma. At the global level, an airframe, a vehicle chassis, or a pressure vessel may be analyzed without representing each connection individually. In such cases, the engineer assumes continuity of load transfer, focusing only on global stiffness or strength. But when certification or safety-critical components are involved, simplification is no longer possible. Local flexibility, stress concentrations, preload effects, and nonlinear behaviors at joints can dominate performance, and ignoring them may lead to unconservative or misleading results.
This section addresses the practical modeling of joints and connections in FEA. It reviews the most common connection types used in aerospace, automotive, and mechanical engineering, explains the physical behavior that governs them, and discusses modeling strategies ranging from simplified connector elements to detailed nonlinear 3D simulations. The aim is not to prescribe one “correct” method, but to provide the practicing engineer with an understanding of the available approaches and the trade-offs between computational cost, accuracy, and relevance to design questions.
Bolts and Rivets Analysis in FEA
Bolts and rivets remain central to structural engineering. Rivets, still the workhorse of airframe construction, distribute loads across large panels and provide redundancy. Bolts, on the other hand, are widely used where clamping and serviceability are required, such as in mechanical joints, pressure boundaries, or structural attachments. Both are deceptively simple in appearance but surprisingly complex in behavior.
From the perspective of FE analysis, the first decision is how much fidelity the joint requires. In large assemblies, where thousands of fasteners exist, it is neither practical nor necessary to model each one explicitly. Instead, engineers frequently rely on equivalent stiffness assumptions or simplified connector elements. A common method is to use spider elements that tie the nodes around a hole to a central node. A rigid spider enforces identical displacements, producing an artificially stiff response. A flexible spider, by contrast, distributes loads more realistically, allowing local compliance and better representing the load path.
Modern FE solvers also offer dedicated “bolt” or “fastener” elements, which are highly effective when simulating large bolt patterns. These elements can capture axial and shear stiffness, some even allowing preload to be specified directly. For global analyses, where the interest is primarily in stiffness distribution or overall load transfer, such simplifications strike an excellent balance between accuracy and computational efficiency.
The challenge comes when the engineer must study local joint behavior. Consider a preloaded bolt in a fatigue-critical application. The preload itself generates a stress field that redistributes the applied load between frictional shear at the interface and direct bearing on the bolt shank. If this preload relaxes in service, the joint may slip, dramatically changing the stress state. Such behavior cannot be captured by simple connector elements. Detailed solid models are required, with explicit representation of the bolt, washer, nut, and clamped parts. Preload can then be applied either as an axial force, through thermal pre-strain, or by simulating the tightening process itself. The latter is computationally expensive but offers the most realistic representation, including the effect of friction and thread contact.
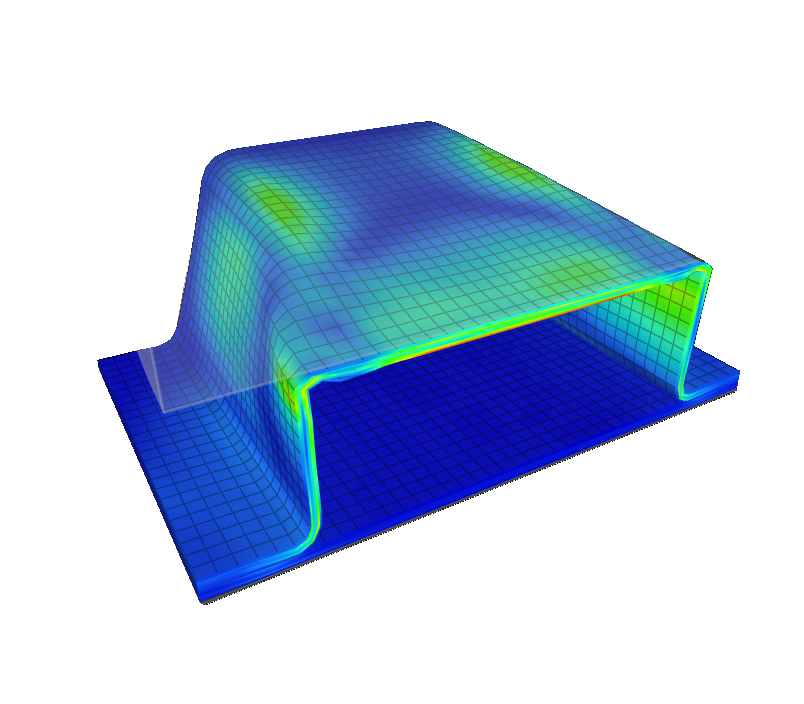
Contact modeling is particularly critical in bolt and rivet analysis. In simplified linear contact, surfaces are assumed to remain in contact under all loading. While efficient, this ignores separation, slip, and frictional effects. Nonlinear contact allows surfaces to open, close, and slide, introducing stiffness nonlinearity and stress redistributions that are often decisive for fatigue life. For rivets and interference-fit bolts, initial overlap between the rivet and the hole can be defined, generating residual compressive stresses that delay crack initiation. Such residual stress fields are difficult to capture otherwise but have major implications for durability.
Fatigue and fracture mechanics add another layer of complexity. Many airframe fatigue-critical locations are at rivet holes, where fretting between sheets and local notch stresses drive crack initiation. Advanced FEA methods, such as cohesive zone modeling or fracture mechanics approaches using Stress Intensity Factors and J-integrals, allow engineers to simulate crack growth. In practice, it is common to calibrate these models against coupon tests or joint-level experiments to ensure that assumptions about friction coefficients, preload, and joint stiffness match reality. For those providing or consuming FEA services, establishing such calibration is critical – without it, even the most sophisticated FE analysis may not align with physical behavior.
Lugs Modelling
Lugs are a quintessential aerospace connection. They are simple in form – a hole in a plate or fitting through which a pin is inserted – yet their structural significance is enormous. Lugs connect control surfaces, landing gear, and major structural members. A single lug failure can lead to catastrophic consequences, which is why they are almost always treated as fatigue-critical items in certification.
In traditional design, lugs are checked against classical failure modes: bearing failure under compressive pin loading, net-tension failure across the reduced section, or shear-out failure along the load line. These checks are conservative and ensure basic strength, but they do not capture the subtle redistributions of stress that occur in reality. For example, a lug with clearance will only transfer load through a partial contact arc, leading to localized overstresses. Similarly, the pin itself may bend under load, altering the bearing pattern and increasing stress near the lug radius.
FEA provides the tools to move beyond these simplified checks. In a first approximation, a lug can be represented using shell elements, with the pin load distributed around the hole through constraints. This approach is computationally efficient and useful for global models, where the main interest is how load flows through a structure rather than precise local stress states. However, this simplification often underestimates peak stresses at the hole edge, and ignores nonlinear contact.
A more realistic strategy is to represent the lug and pin with solid elements, explicitly defining the contact between them. This allows the analysis to capture how the pin presses into the lug, how the contact patch evolves as load increases, and how clearance or interference changes the response. Nonlinear contact with friction becomes essential, since in service pins rarely behave as frictionless, perfectly fitting cylinders. Instead, they experience micro-slip, edge contact, and even local plasticity. Only a nonlinear model can capture such phenomena.
Interference fits deserve special mention. Many aerospace lugs are designed with pins installed under slight interference to generate beneficial compressive hoop stresses around the hole. These residual stresses delay crack initiation and increase fatigue life. Accurately capturing this effect in FEA requires careful modeling of initial overlap and elastic-plastic material behavior. When done correctly, the simulation provides invaluable insight into both the static and fatigue performance of the lug.
When fatigue life is under scrutiny, engineers turn to fracture mechanics. Stress Intensity Factor evaluation at critical points allows prediction of crack growth rates under cyclic loading. More advanced approaches, such as extended finite element methods (XFEM), allow cracks to initiate and propagate directly in the model without remeshing. This has proven extremely powerful in the aerospace sector, where regulatory authorities demand demonstration of safe crack growth behavior in lugs.
Welds
Welded joints are among the most widely used connection types in mechanical and automotive structures. Unlike bolts or rivets, welds are continuous connections, often carrying load across significant lengths. However, they are also prone to stress concentrations, residual stresses, and fatigue cracking, particularly at the weld toe or root.
In FE analysis, the first challenge is deciding the level of detail. A global chassis model, for example, may treat welds simply as line constraints, ensuring that load is transmitted between parts. This is efficient and often sufficient for stiffness studies. But for durability or fatigue assessments, weld representation must be more refined.
One approach is to use shell elements with tied connections along the weld line. This ensures load transfer while keeping the model efficient. For higher fidelity, solid elements can represent the actual weld geometry, including fillets and penetration profiles. This allows the stress concentration at the weld toe to be resolved, which is often where fatigue cracks initiate. The difficulty is that real weld geometries are highly irregular, and modeling them in detail across an entire structure is impractical.
To address this, engineers often employ the “hot spot” method. Instead of modeling the weld toe geometry explicitly, stresses are extracted at defined points near the weld, and fatigue assessment is based on these “hot spot” stresses. This method is widely accepted in design standards such as IIW and provides a pragmatic compromise between accuracy and computational effort.
Residual stresses from welding also play a significant role. Thermal cycles during welding create tensile residual stresses that reduce fatigue life. Advanced FEA can simulate the welding process itself, including heat input, cooling, and phase changes, but such models are computationally heavy and generally reserved for research or critical applications. In practice, many design engineers rely on simplified residual stress assumptions, applying them as initial conditions in fatigue analyses.
Bonded Joints
Adhesive bonding has become increasingly important in modern structures, particularly in aerospace composites and lightweight automotive assemblies. Bonded joints offer smooth load transfer, eliminate the need for mechanical fasteners, and reduce stress concentrations. However, they introduce new challenges in both design and simulation.
From the perspective of FEA, bonded joints can be modeled in several ways. Thin adhesive layers can be represented using cohesive elements, which define a traction–separation law. This approach allows progressive damage and failure to be simulated, making it ideal for durability and crashworthiness studies. In cases where the adhesive layer is very thin relative to the adherends, engineers may approximate it using shell elements with reduced stiffness or by applying contact with defined shear and normal behavior.
Cohesive Zone Modeling (CZM) has become a standard tool for adhesive simulation. In CZM, the adhesive behaves linearly up to a critical stress, after which stiffness degrades until full separation occurs. This captures the progressive nature of adhesive failure, which is rarely instantaneous. Another powerful method is the Virtual Crack Closure Technique (VCCT), which evaluates energy release rates to predict crack growth along an adhesive interface. Both approaches are widely implemented in commercial FE solvers and form the backbone of bonded joint analysis in FEA services today.
As with welds, the level of detail depends on the analysis objective. In large assembly models, bonded joints may be represented simply as tied contacts, ensuring continuity. For certification-level analyses, however, the adhesive must be represented explicitly, with careful calibration of cohesive laws against experimental data. Adhesives are highly sensitive to temperature, humidity, and aging, so validation against physical tests is essential if the FE model is to provide reliable predictions.
Flexible and Damped Connections
Not all connections are rigid or intended to provide purely structural continuity. Many mechanisms rely on connections that are deliberately flexible, compliant, or damped in order to transmit loads while accommodating motion or absorbing vibration. Examples include elastomeric bushings in automotive suspensions, flexible couplings in rotating machinery, and vibration isolators in aerospace equipment mounts. Unlike bolts, rivets, or welds, these connections are designed as functional components in their own right, rather than as near-rigid attachments.
From an FEA perspective, flexible connections introduce both opportunities and challenges. Their primary role is often to filter loads and vibrations, which means their behavior is dominated by stiffness, damping, and in some cases frequency-dependent viscoelastic effects. Representing them as rigid or perfectly elastic would entirely miss their engineering purpose.
The most straightforward approach is to use spring or bushing elements available in most commercial FE solvers. These allow directional stiffness to be specified independently in translation and rotation. For example, an automotive suspension bushing can be represented with high stiffness in the vertical load path, moderate stiffness laterally, and very low stiffness in rotation about a particular axis. Damping can be added as viscous coefficients, enabling the model to reproduce not only static compliance but also dynamic attenuation of vibrations.
For more advanced cases, particularly where large deformations or nonlinear material behavior is relevant, the flexible connector itself can be modeled as a solid continuum with appropriate constitutive laws. Elastomeric components may require hyperelastic material models such as Mooney-Rivlin or Ogden formulations, and if hysteresis or rate-dependence is important, viscoelastic properties must be included. This is common in aerospace isolators, where the time-dependent response governs vibration transmission into sensitive equipment.
Another practical consideration is the interaction between flexible connectors and surrounding rigid structure. In many mechanisms, the compliance of bushings or dampers allows redistribution of loads across multiple paths. Capturing this correctly in FE analysis may require a combination of simplified directional springs for system-level models and detailed solid material models for component-level studies. Calibration against experimental stiffness and damping curves is essential, since small errors in connector properties can propagate into large discrepancies in predicted dynamic response.
Flexible and damped connections highlight the broader role of FE analysis beyond static strength evaluation. They demonstrate how joints can be modeled not only as structural weaknesses to be managed, but also as functional elements to be optimized for noise, vibration, harshness (NVH), fatigue, and comfort. In modern mechanical and automotive design, mastering this aspect of joint modeling is just as important as predicting bolt preload or weld toe stresses.
Conclusion
Joints and connections are among the most challenging aspects of FE analysis. They are small compared to the overall structure, yet their behavior often governs stiffness, strength, durability, and dynamic performance. Bolts and rivets require careful treatment of preload and contact; lugs demand nonlinear analysis and sometimes fracture mechanics; welds bring issues of residual stress and stress concentration; bonded joints require progressive failure modeling; and flexible connectors add another layer, where frequency-dependent compliance and damping must be captured accurately to predict real-world performance.
For the practicing engineer, the central question is always: how much fidelity is necessary? Simplified representations may suffice for global stiffness or load-path analysis, while safety-critical or fatigue-critical applications demand nonlinear 3D detail. Flexible and damped connections add further nuance, since their purpose is not just to hold components together but to actively tune load transfer and vibration response.
In every case, validation against experimental data is indispensable. Preload, friction, damping, and material nonlinearity are difficult to capture purely from theory, and without calibration, even sophisticated FE models may diverge from reality.
By understanding the physics of both rigid and flexible connections, and by choosing modeling strategies appropriate to each design question, engineers can harness FEA not only as a tool for global structural analysis but also as a predictive framework for local failure, fatigue life, and vibration performance. For organizations offering or consuming FEA services, mastery of these modeling methods is a decisive capability, enabling efficient and accurate design validation across aerospace, automotive, and mechanical engineering.