A Short Review of Buckling and Stability Analysis using FEA
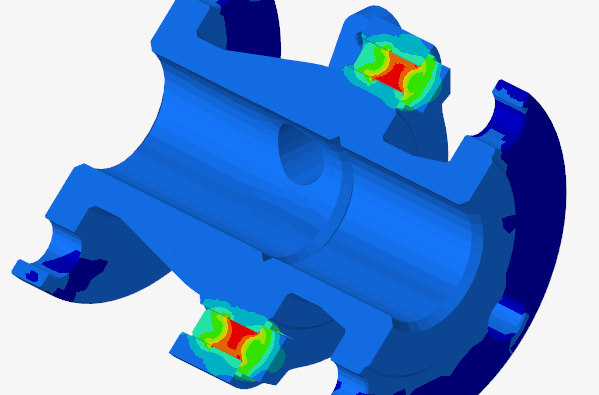
Buckling stability analysis is a critical branch of finite element analysis (FEA) focused on predicting when a structure loses stability under compressive or shear loading. Unlike simple strength validation, buckling is a geometric instability that can occur at stress levels well below the material’s yield strength. Advanced finite element simulation techniques are required to capture both the onset of instability and the post-buckling behavior of slender or thin-walled structures.
For experienced engineers, buckling simulation is about more than finding a critical load factor. Nonlinear FEA is used to study imperfection sensitivity, mode interaction, and load redistribution, while advanced solvers trace equilibrium paths deep into the post-buckling regime. This makes buckling finite element analysis indispensable for aerospace, civil, offshore, and energy industries where lightweight, high-performance structures must operate safely near their stability limits.
Typical Goals and Targets in Buckling Simulation with FEA
The primary goal of buckling analysis in structural simulation is to identify the critical loads and mode shapes that can trigger instability. Linear eigenvalue FEA provides an initial estimate of idealized buckling loads, but senior analysts know that real-world imperfections, residual stresses, and material plasticity must be included for meaningful predictions.
With nonlinear finite element analysis, engineers simulate realistic imperfection sensitivity and quantify knockdown factors for certification. Post-buckling simulations provide insights into whether a structure has reserve strength beyond the initial instability or collapses immediately. These targets make buckling FEA essential for safety-critical systems, weight optimization, and compliance with international codes.
Core Modeling Dimensions in Buckling Stability Analysis
Linear eigenvalue buckling predicts critical load factors by solving a generalized eigenvalue problem. While efficient, it assumes perfect geometry and elastic material behavior, making it optimistic. Nonlinear buckling accounts for large deformations, plasticity, and contact, providing more realistic but computationally intensive results. Expert analysts often run both: linear for identifying potential modes, nonlinear for assessing real-world stability margins.
Most buckling is evaluated in static simulations, but transient dynamic buckling can occur under short-duration pulses (e.g., blast, seismic, or crash events). Explicit solvers are used for dynamic buckling, capturing inertia effects and snap-through behavior. For advanced engineers, recognizing when a static bifurcation assumption breaks down is essential for accurate prediction.
Implicit solvers dominate quasi-static buckling simulations in structural FEA, especially when combined with arc-length (Riks) methods to trace post-buckling paths. Explicit solvers are valuable for highly nonlinear, dynamic buckling problems where implicit methods struggle to converge. Expert simulation engineers select solvers strategically based on load application speed, stability requirements, and computational efficiency.
Elastic buckling assumes ideal materials, but real-world cases demand inclusion of plasticity, creep, or orthotropic behavior. In thin metallic shells, plastic collapse often coincides with buckling, requiring elastic–plastic formulations. Composite panels demand orthotropic stiffness and failure criteria, since fiber misalignment or ply drop-offs can dominate instability. Experts often calibrate models with coupon and subcomponent tests to validate these complex material responses.
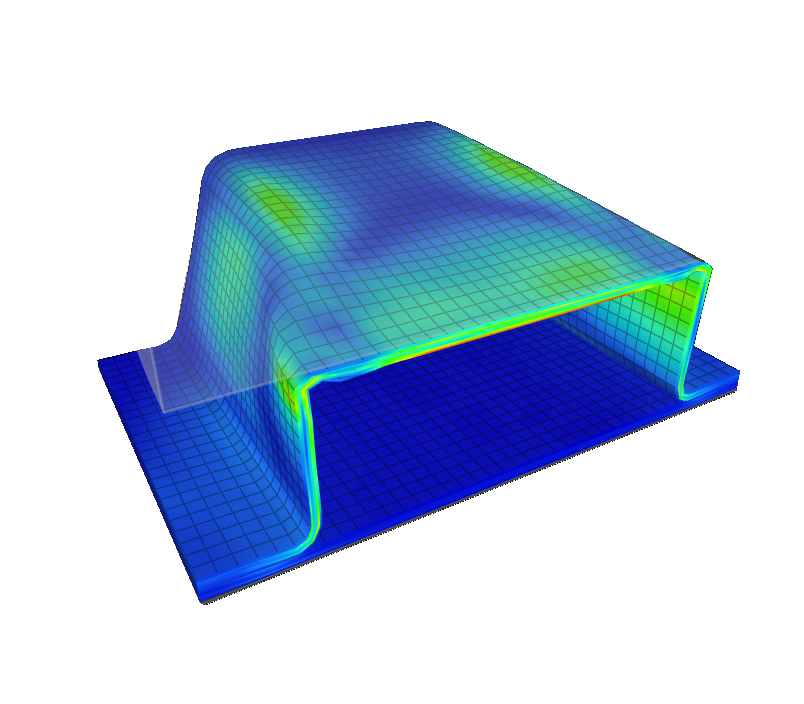
Slender columns can be idealized with beam elements, while shells and stiffened panels require shell formulations with sufficient refinement. Solid elements may be necessary in transition zones or for local buckling modes. Imperfection modeling is critical: introducing small geometric deviations (e.g., first buckling mode scaled to 0.1–1% of thickness) often shifts predicted critical loads closer to experimental values.
Buckling rarely occurs in isolation. Thermal gradients can induce compressive stresses leading to thermal buckling, while aerodynamic loading can cause flutter or aeroelastic instability. Offshore structures may require hydrostatic pressure–induced buckling combined with material plasticity. Multiphysics buckling simulations are increasingly essential for certification in aerospace, energy, and civil domains.
Deterministic eigenvalue buckling is insufficient for safety-critical structures. Probabilistic buckling accounts for uncertainties in geometry, thickness, residual stresses, and material variability. Knockdown factors derived from stochastic analyses are often significantly lower than deterministic predictions, and they guide conservative design margins in aerospace standards (e.g., NASA SP-8007 for shell buckling).
One-dimensional beam models capture global buckling of trusses, while 2D shell models resolve local skin instability in panels. Full 3D continuum models become necessary when local buckling couples strongly with global deformation. Expert engineers use hierarchical modeling: starting from reduced-order models and progressing to refined 3D models where nonlinear interactions dominate.
Frequency-domain eigenvalue buckling identifies bifurcation points but not post-buckling paths. Time-domain methods (e.g., transient explicit) simulate snap-through or collapse under dynamic excitation. For slender shells, time-domain approaches capture mode switching and imperfection sensitivity better than eigenvalue methods alone.
Automation is increasingly used to scan multiple imperfection scenarios, load cases, and boundary conditions. Optimization workflows adjust stiffener spacing, skin thickness, or frame geometry to maximize buckling capacity while minimizing weight. Surrogate models trained on FE results allow rapid exploration of imperfection sensitivity, supporting robust lightweight design.
Convergence is notoriously challenging in nonlinear buckling. Experienced engineers use arc-length control, automatic stabilization, and adaptive meshing to follow unstable equilibrium paths. Monitoring energy balance and eigenvalue shifts provides insight into when a simulation captures true physical instability versus numerical artifacts.
Most buckling studies use continuum elements, but discrete joint models may be necessary in lattice or truss structures where instability arises from connector flexibility. In fracture–buckling interaction problems, XFEM or cohesive models simulate crack initiation during instability. Hybrid approaches combining continuum shells with discrete connectors often yield the most realistic predictions.
Typical Mistakes in Buckling Analysis and How to Avoid Them
Common errors include overreliance on linear eigenvalue results, failure to introduce imperfections, and neglecting residual stresses. These mistakes often lead to unsafe overpredictions of critical loads. Another pitfall is insufficient mesh refinement in thin shells, which can suppress or distort buckling modes.
To avoid these issues, engineers should always perform imperfection studies, validate against experimental knockdown factors, and run nonlinear analyses for critical cases. Using multiple modeling scales — from beam to full 3D — helps cross-check consistency. Convergence studies and sensitivity checks are indispensable in ensuring stability predictions are not numerical artifacts.
Your Simulation Project with FiniteNow
Use Cases of Buckling Simulation with FEA
Aerospace Shell Panel Buckling
Thin composite fuselage panels are prone to local buckling under compression. Nonlinear buckling simulations, including imperfections and ply-level orthotropy, provide accurate safety margins. These results are used for both certification and structural optimization, reducing unnecessary weight.
Offshore Pipeline Collapse under Hydrostatic Pressure
Subsea pipelines face external hydrostatic loading that can induce ovalization and collapse. Advanced nonlinear buckling analyses capture interaction between ovality imperfections, residual stresses, and plastic collapse. This ensures pipeline integrity under deep-water conditions.
Civil Engineering – Column and Frame Stability
High-rise building columns and long-span bridges require global and local buckling checks. Eigenvalue analysis identifies potential modes, while nonlinear pushover analyses ensure realistic predictions under combined loads. Engineers validate models with code-based knockdown factors and structural monitoring data.
Learn more about our portfolio of Structural Engineering Services
FAQ – Buckling Stability Analysis in Structural Simulation
It is the study of structural instability under compressive or shear loads, where a component suddenly loses load-carrying capacity. Unlike yielding, buckling is a geometric failure mode, often occurring at stresses well below material strength. Predicting it accurately requires specialized finite element methods.
Linear eigenvalue analysis assumes perfect geometry and elastic behavior, producing optimistic load predictions. Real-world imperfections, residual stresses, and material nonlinearities reduce actual buckling strength significantly. Nonlinear and imperfection-seeded models provide more conservative and realistic results.
Imperfections are introduced as small geometric deviations, often scaled from the lowest buckling eigenmodes. Even tiny deviations can drastically lower critical loads, especially in thin shells. Including imperfections bridges the gap between idealized theory and experimental reality.
Dynamic buckling applies when loads are applied rapidly, such as blast, seismic, or crash scenarios. Explicit solvers capture inertia effects, mode switching, and snap-through collapse. Advanced engineers recognize that static assumptions may fail for these transient cases.
Arc-length (Riks) methods allow tracing post-buckling equilibrium paths, while standard load incrementation may diverge after bifurcation. Stabilization and adaptive meshing help avoid non-convergence. Choosing solver settings is critical for capturing true physical behavior.
Elastic-only models predict idealized buckling, but real-world collapse often involves plasticity. Elastic–plastic models capture load redistribution and collapse loads. In composites, orthotropy and progressive failure models are essential for realistic buckling prediction.
Buckling modes are highly mesh-sensitive, particularly in thin shells. Insufficient refinement suppresses higher-order modes or introduces numerical artifacts. Convergence studies with mesh refinement are mandatory for credible results.
Post-buckling analysis traces load-displacement response beyond initial instability. This helps determine whether a structure exhibits stable post-buckling reserve strength or immediate collapse. Expert analysts use arc-length methods and imperfection sensitivity studies to capture this regime.
FiniteNow.com provides instant quoting, eliminating delays in critical project planning. Its scalable network of senior FEA specialists ensures expertise in nonlinear buckling, imperfection modeling, and multiphysics stability. By leveraging pre-audited providers, FiniteNow balances speed, cost efficiency, and advanced technical quality.
Monte Carlo or stochastic methods are used to account for variability in thickness, material properties, and imperfections. This provides probability distributions of buckling loads rather than a single deterministic value. Such methods underpin robust design practices in aerospace and offshore engineering.
Validation involves subcomponent testing, imperfection measurement, and correlation with nonlinear simulations. Knockdown factors are applied to bridge gaps between test data and predictions. Expert engineers ensure that both model fidelity and safety margins are consistent with certification requirements.
Current frontiers include machine-learning–assisted imperfection sensitivity studies, reduced-order modeling of large shell assemblies, and multiphysics buckling involving thermal and aeroelastic effects. These methods aim to accelerate simulations while maintaining predictive fidelity. For experts, integrating these approaches into industrial workflows is the next step toward digital certification.
Start Now! It will only take 12 minutes
It has never been faster, easier and more cost effective to get a quotation for your structural simulation needs: