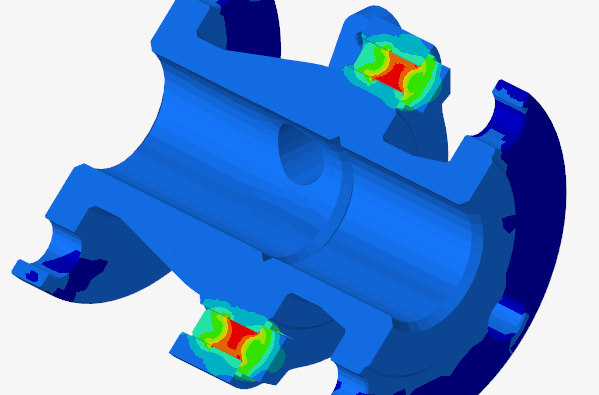
Evaluation of Strength and Stress in Brief
Strength and stress analysis is one of the most widely applied forms of structural simulation. It evaluates how materials and structures respond to external forces, ensuring that stresses remain below critical thresholds and that safety factors are met. By calculating detailed stress fields, engineers can detect weak points, prevent material failure, and validate that designs comply with industry standards before manufacturing begins.
Modern finite element analysis (FEA) enables the simulation of both simple parts and large assemblies under complex load combinations. It can capture local stress peaks at notches or holes, evaluate load distribution in joints, and assess whether components will yield, fracture, or fatigue over time. This makes stress analysis essential for industries ranging from automotive and aerospace to civil engineering, energy, and consumer products.
Typical Goals and Targets in Strength and Stress Simulation
The primary goal of structural stress analysis is to ensure that components and assemblies can safely carry the loads they are designed for without permanent deformation or catastrophic failure. Engineers perform these simulations to check that stresses remain below material limits (yield strength, ultimate tensile strength, fatigue strength) under normal and extreme conditions. This verification process is critical for safety, product reliability, and compliance with design codes and certification standards.
Our Core Modeling Strategies in Stress and Strength Analysis
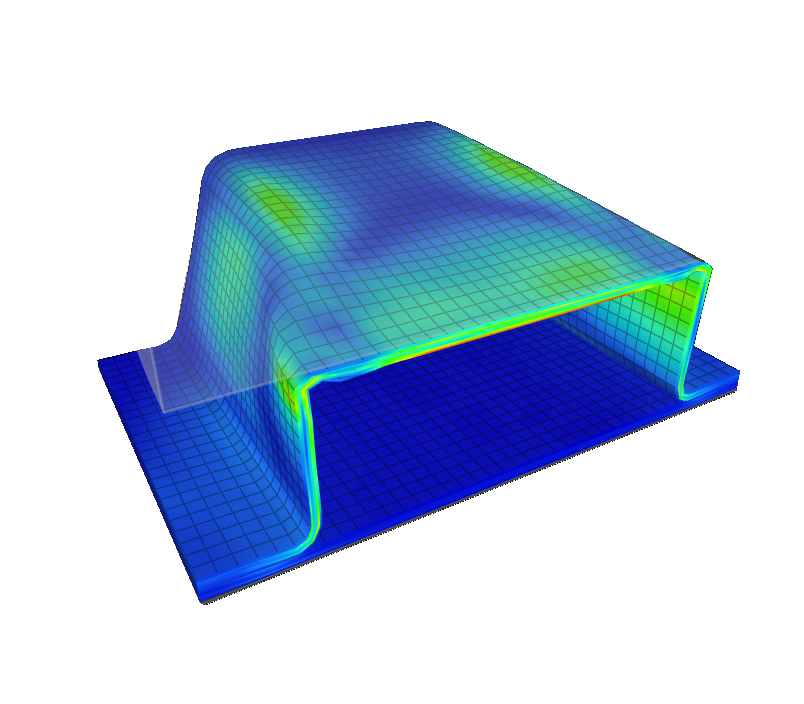
Linear stress simulations assume small deformations and elastic material behavior, making them fast and widely used for early design validation. They can quickly confirm whether stresses stay below allowable levels under simple load cases. However, in real-world applications where plasticity, large deformations, or complex contact interactions occur, nonlinear stress analysis is required. Nonlinear models can capture yielding, stress redistribution, and ultimate failure more realistically, but they demand more computational power and careful setup. Engineers often begin with linear runs for initial screening, followed by nonlinear refinements for critical load cases.
Stress analysis can be conducted under static loading, representing constant service conditions, or in a transient framework where stresses evolve over time. Static analysis is ideal for components subject to steady loads, such as pressure vessels or support beams. Transient stress simulations are essential for scenarios like startup of rotating machinery, thermal shock, or impact loading. Capturing stress evolution over time helps identify not only peak stress levels but also cumulative effects, such as creep or low-cycle fatigue. In advanced applications, coupled thermo-mechanical or vibration-induced stresses may require transient multiphysics approaches.
Implicit solvers are the standard choice for most stress analyses, offering stability and efficiency in static or slow transient simulations. They are well-suited for verifying structural strength under operating loads, pressure, or thermal expansion. Explicit solvers are preferred in cases where stress evolves during very fast, dynamic events such as crashes, ballistic impacts, or explosions. Explicit methods allow for highly nonlinear material models and complex contact interactions but require very small time steps. The choice between implicit and explicit directly influences accuracy, computational cost, and the ability to simulate extreme scenarios.
The accuracy of stress predictions depends heavily on the fidelity of the material models. Linear elastic materials are sufficient for many metals at low stress levels, but plasticity models are required when yield or hardening occurs. For polymers and composites, nonlinear, viscoelastic, or orthotropic models must be used to capture true strength behavior. Advanced simulations may incorporate creep, fatigue degradation, or fracture mechanics, particularly in aerospace or energy applications. Material testing and calibration are critical for ensuring the model represents reality – otherwise, the predicted stress fields may be misleading.
Geometric fidelity plays a large role in FEA stress analysis. Stress concentrations often occur at fillets, holes, welds, or notches, requiring fine local mesh refinement. Engineers may simplify non-critical geometry to reduce computation time while maintaining detail in high-stress areas. For thin-walled structures, shell elements provide efficient yet accurate stress predictions, while 3D solid elements capture local effects in complex regions and 3D stress states. Hybrid models often combine different element types to balance accuracy and performance. Proper representation of joints and contact surfaces is particularly important since they strongly influence load distribution.
Many stress problems are influenced by other physical domains. Thermo-mechanical coupling evaluates stresses caused by thermal expansion or gradients, which can be critical in engines, turbines, and electronics. Fluid-structure interaction (FSI) captures how fluid pressure and flow-induced forces affect stress levels in thin-walled structures or seals. In electromagnetically loaded systems, Lorentz forces or Joule heating must be included. Coupled multiphysics stress simulations give a more complete picture of real-world operating conditions but require specialized solvers and greater computational resources.
Traditional stress analysis is deterministic, assuming fixed material properties, loads, and boundary conditions. In reality, variations exist in manufacturing tolerances, load distributions, and material strengths. Probabilistic stress analysis uses statistical methods or Monte Carlo simulations to account for these uncertainties as input parameters for FEA models. This enables engineers to assess not just whether a design meets requirements, but with what probability it will fail or succeed. Reliability engineering and safety-critical industries rely on probabilistic stress validation to build robust, fail-safe systems.
Stress analysis can be conducted at multiple levels of dimensional complexity. 1D beam and truss models are useful for quick load-path checks in large structures. 2D plane stress or plane strain models simplify prismatic or axisymmetric geometries. Full 3D finite element models are required for detailed analysis of complex parts or joints. The choice depends on the required accuracy, computational resources, and the criticality of the design. A staged approach often begins with simple 1D/2D models before moving to full 3D simulations for final validation.
Stress can also be studied in the frequency domain, particularly when related to vibration. Modal stress analysis identifies resonant frequencies and stress amplification due to resonance. Harmonic and random vibration analyses predict stress responses under oscillatory loads such as road-induced vibrations or engine excitations. Time-domain analysis, on the other hand, is necessary for transient or non-repetitive events. Combining frequency- and time-domain methods provides a comprehensive understanding of structural stress behavior.
Automation streamlines repetitive stress analysis tasks in our FE-Suites, such as evaluating multiple load cases or design variations. Parametric studies allow engineers to quickly see how changing thickness, material, or geometry affects stress levels. Optimization techniques use these simulations to minimize weight while ensuring stress remains below allowable limits. Advanced workflows combine optimization with topology design, generating innovative load-bearing structures. Automated reporting ensures traceability and supports certification documentation.
Stress simulations vary in numerical complexity, requiring careful solver strategy selection. For small models, direct solvers provide robust and accurate results. For large-scale assemblies, iterative solvers significantly reduce computation time while maintaining accuracy. Convergence control, load incrementation, and adaptive meshing strategies are critical in nonlinear stress problems. Expert users monitor energy balance and residual errors to ensure numerical stability and reliability of results.
Most stress analyses rely on continuum mechanics, modeling materials as continuous media. However, in fracture, crack propagation, or granular material problems, discrete approaches may be required. Cohesive zone models and extended finite element methods (XFEM) allow simulation of crack initiation and growth. Discrete element methods (DEM) may be used when stress transfer occurs through granular or jointed materials. Hybrid approaches combine continuum stress models with discrete failure models for greater accuracy in predicting structural failure.
Typical Mistakes in Stress/Strength Analysis and How to Avoid Them
Common mistakes include applying unrealistic boundary conditions, neglecting stress concentrations, and relying on overly coarse meshes. Assuming isotropic material behavior when anisotropy is significant, such as in composites, can lead to critical errors. Another frequent oversight is ignoring preload or residual stresses from manufacturing, which can significantly affect strength predictions.
To avoid these pitfalls, engineers should perform sensitivity analyses, mesh convergence studies, and validate simulations against analytical or experimental benchmarks. Including real-world conditions such as assembly tolerances, thermal effects, and surface treatments improves the reliability of results. Cross-checking simple hand calculations against detailed simulations ensures consistency and builds confidence in the analysis.
Your Stress and Strength Project with FiniteNow
Use Cases of Structural Stress and Strength Analysis
Verification of Pressure Vessel Integrity
Stress analysis ensures that pressure vessels meet code requirements (ASME, EN) by evaluating stresses under internal pressure, thermal gradients, and external loads. High-stress regions at nozzles, welds, and support attachments are carefully studied to avoid catastrophic failure. This validation is essential for safety in chemical, energy, and oil & gas industries.
Load Path Optimization in Aerospace Structures
Aircraft wings, fuselage sections, and landing gear are optimized using stress analysis to balance weight and strength. Simulations identify primary load paths and areas where material can be reduced without compromising safety. This enables significant weight savings, contributing directly to fuel efficiency and cost reduction.
Durability Assessment of Automotive Components
From suspension arms to engine mounts, stress analysis predicts whether components can survive millions of cycles under real-world driving conditions. High-cycle fatigue life predictions rely on accurate stress fields generated by FEA. Early detection of critical stress hotspots allows design changes before expensive physical durability tests are conducted.
Learn more about our portfolio of Structural Engineering Services
FAQ – FE based Stress and Strength Analysis in Structural Simulation
Structural stress analysis is the process of predicting stress distribution in a component or assembly under applied loads. It ensures that stresses remain below allowable limits, preventing failure and maintaining product safety. Without this analysis, designs may appear functional but fail prematurely in service.
Stress analysis focuses on internal forces per unit area within materials, while stiffness or strain analysis looks at deformation and displacement. A component can be stiff but still overstressed, or vice versa. Combining both perspectives provides a complete understanding of structural performance.
Stress simulations cover static loading, thermal stresses, vibration-induced stresses, fatigue life, buckling, and fracture mechanics. They are applied in nearly every industry to validate safety, performance, and durability. Advanced methods also predict stress redistribution during plastic deformation and crack growth.
Popular FEA packages include ANSYS, Abaqus, Nastran, and COMSOL. Each offers specialized solvers for different stress problems, such as nonlinear plasticity or fracture mechanics. Open-source alternatives like CalculiX are used for academic or niche applications.
Accuracy depends on model fidelity, material data, and boundary condition realism. With validated inputs and mesh refinement, simulations can closely match experimental results. However, physical testing is often required for final certification, with simulation used to reduce prototype numbers and guide design.
Linear stress assumes elastic materials and small deformations, providing quick results for many applications. Nonlinear analysis includes plasticity, large deformations, and contact effects, producing more realistic results for complex cases. Engineers typically use linear runs for early checks and nonlinear runs for final validation of critical cases.
Stress concentrations occur at geometric discontinuities such as holes, notches, and welds. These areas often control the fatigue life of components. Simulations help identify critical locations and guide design modifications such as fillet radii increases, reinforcement, or material selection.
Fatigue prediction uses stress results combined with S–N curves or strain-life methods. Critical stress ranges and load cycles are used to estimate the number of cycles to failure. Accurate fatigue prediction requires both realistic loading histories and validated material fatigue properties.
FiniteNow.com provides instant quoting, enabling projects to start without long delays. Its network of pre-audited simulation experts ensures that specialized knowledge is applied to each case, whether it’s weld fatigue, thermal stress, or high-cycle fatigue. The scalable model keeps costs competitive while maintaining top engineering quality.
FiniteNow.com provides instant quoting, enabling projects to start without long delays. Its network of pre-audited simulation experts ensures that specialized knowledge is applied to each case, whether it’s weld fatigue, thermal stress, or high-cycle fatigue. The scalable model keeps costs competitive while maintaining top engineering quality.
Advanced users manage nonlinear convergence by refining load steps, using adaptive meshing, and applying stabilization techniques. Monitoring energy balance and residual forces helps ensure stability. Experienced analysts know how to balance numerical efficiency with accuracy in highly nonlinear stress problems.
Fracture mechanics extend stress analysis by predicting crack initiation and growth. Methods like XFEM or cohesive zone modeling allow simulation of crack propagation under load. These approaches are crucial in safety-critical industries such as aerospace, nuclear, and pressure vessel design.
Probabilistic methods account for variability in loads, materials, and manufacturing tolerances. By running multiple simulations with statistical input distributions, engineers can calculate the probability of failure instead of relying on a single deterministic result. This supports robust design and risk-based decision-making.
Start Now! It will only take 12 minutes
It has never been faster, easier and more cost effective to get a quotation for your structural simulation needs: